Interessanti problemi con la mappa

Don Knuth sta lavorando al Volume 4 dell'Arte della Programmazione del Computer. Uno dei capitoli è su Diagrammi decisionali binari e le loro applicazioni, un argomento che trovo molto interessante. Knuth mostra che una varietà di problemi grafici interessanti possono essere codificati come formule booleane, e il BDD derivato rappresenta tutte le possibili soluzioni al problema. Spesso esiste una sorta di criterio di ottimizzazione ed è abbastanza facile estrarre la soluzione "migliore" dal BDD con un semplice algoritmo di programmazione dinamica.

Qui mostriamo alcuni esempi, utilizzando il grafico che rappresenta i 48 stati contigui, con un nodo per ogni stato e un margine tra due stati se condividono un confine. Per ciascuna delle mappe, se si fa clic sull'immagine di lui si raggiunge il documento di origine in formato SVG. Ecco il grafico, individuando i nodi nelle capitali degli stati:

Capital Tours (giro del capitale)

Supponiamo che tu voglia visitare la capitale di 48 stato con il requisito che tu passi solo attraverso ogni stato una volta. (In altre parole, vuoi trovare un percorso hamiltoniano nel grafico.) Come puoi vedere dalla mappa sopra, se segui la rotta più diretta tra le capitali dello stato, passerai spesso attraverso un altro stato, o nel caso di andando da Lansing, Michigan a Madison, Wisconsin, attraverserai il lago Michigan. Invece, dovresti prendere il percorso di guida più breve che rimane nei due stati per ogni tappa del viaggio. Chiamiamo un itinerario del genere come un giro del capitale. Ecco uno schema dei percorsi consentiti tra gli stati:

Sulla base di una semplice analisi, oltre agli sforzi di Knuth, possiamo dire quanto segue:

Tutti tours devono iniziare o finire nel Maine, dal momento che il Maine ha un solo vicino. Useremo il Maine come punto di partenza.
Tutti tours devono finire oltre New York, poiché è un punto di articolazione.

Ci sono 68.656.026 diversi tour di capitale in generale.

Ecco la più breve visita in capitale(capital tour), per un totale di 11.698 miglia:

Ecco il tour più lungo della capitale(capital tour), 18.040 miglia in totale:

Colorazione del grafico

Un'altra interessante classe di problemi riguarda la colorazione della mappa. La regola è che nessuno degli stati adiacenti può avere lo stesso colore. Il famoso Teorema dei quattro colori afferma che qualsiasi grafico planare può essere colorato con al massimo quattro colori.

Dal momento che un BDD codifica tutte le soluzioni possibili a una formula booleana, possiamo facilmente calcolare quante soluzioni ci sono. Per la colorazione del grafico, regoliamo i nostri conteggi per eliminare le simmetrie dovute all'assegnazione arbitraria dei valori dei colori (4! Casi simmetrici per la colorazione a 4).

Per colorare i 48 stati contigui, ci sono 533.816.322.048 colorazioni possibili. (Questo è 1/2 il numero riportato da Knuth, dal momento che la sua mappa include Washington, DC come 49 ° "stato", e può essere assegnato uno dei due colori non usati per Maryland e Virginia.) Ecco alcuni esempi interessanti di coloranti speciali:

Una colorazione equilibrata, in cui ogni colore è usato per esattamente 12 stati. Ci sono 12.554.677.864 coloranti di questo tipo, che è sorprendentemente alto il 2,4% di tutti i coloranti possibili:
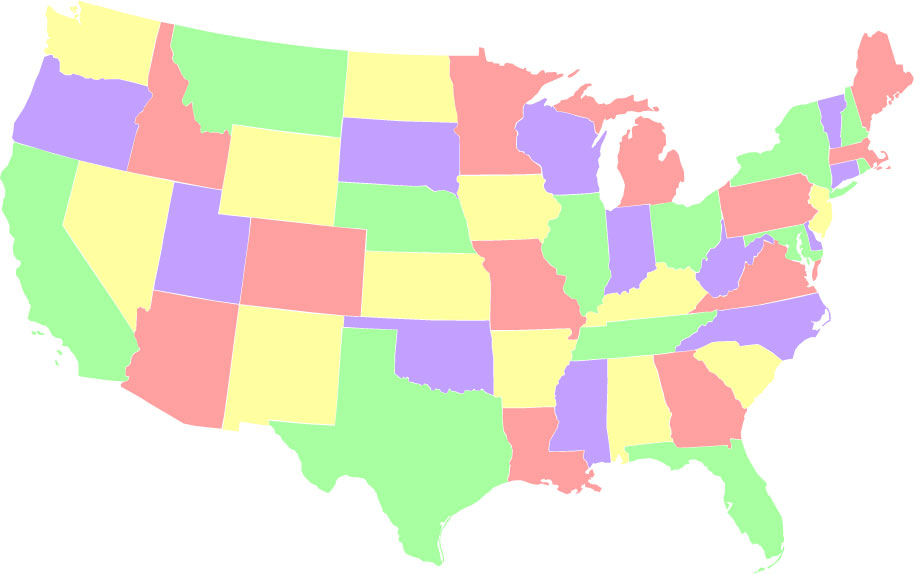
Una colorazione sbilanciata, in cui uno dei colori (verde) viene usato il meno possibile (2 stati). Ci sono solo 288 modi per colorare la mappa in modo tale che un colore venga usato solo due volte.
Una colorazione sbilanciata, in cui uno dei colori (giallo) è usato il più possibile (18 stati). Ci sono 71,002,368 modi per colorare la mappa in modo tale che un colore venga usato 18 volte.
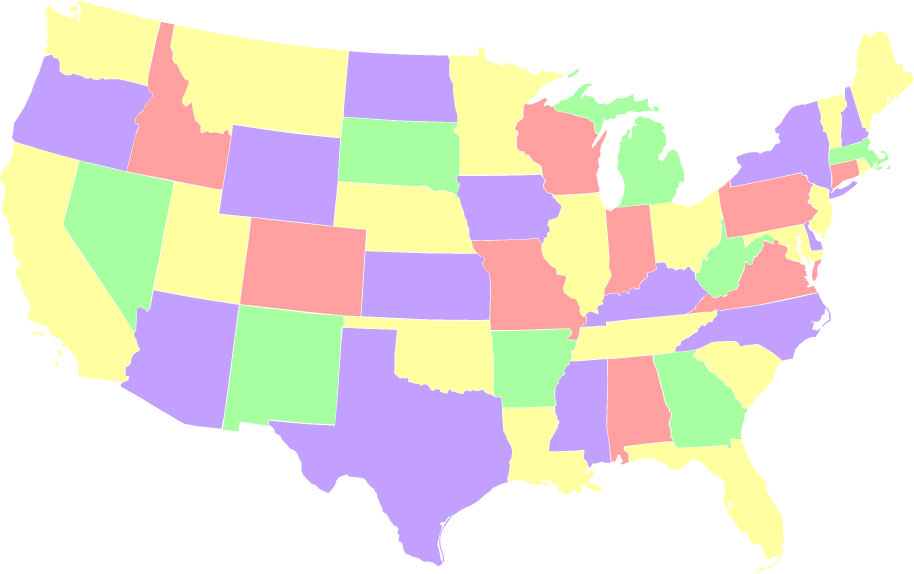
Combinando entrambi. Coloranti con i colori 2, 13, 15 e 18 volte. Questa sequenza 1) da sinistra a destra, utilizza ciascun colore in successione per il minor numero di volte possibile, e 2) da destra a sinistra, utilizza ciascun colore in successione per il maggior numero di volte. Ci sono 24 soluzioni di questo tipo.

Dalla prospettiva dei programmi di colorazione dei grafici, la mappa degli 48 Stati dei USA è abbastanza semplice. Per una mappa più impegnativa, vedere la pagina Web sul grafico di McGregor.